|
|
|
The word “Squircle” was coined
by Peter Panholzer in the summer of 1966 in |
|
As an aspiring architect born and
studying in |
|
The mathematical equation of the
Superellipse was not invented by Piet Hein, but by Gabriel Lamé. https://en.wikipedia.org/wiki/Gabriel_Lam%C3%A9 |
|
According to
Gabriel Lamé in 1818, the Superellipse follows the modified formular for the ellipse, (x/a)n
+ (y/b)n = 1, where the
power of 2 is increased to a higher number. Piet Hein used an arbitrary
relatively low exponent n of 2.6 for his urban design
pattern. Peter asked himself, why should one be
eyeballing the resulting shape for aesthetic
or practical effect. Simplifying the problem he settled on the special case
of a circle instead of an ellipse (which
Piet Hein also did and dubbed a Supercircle).
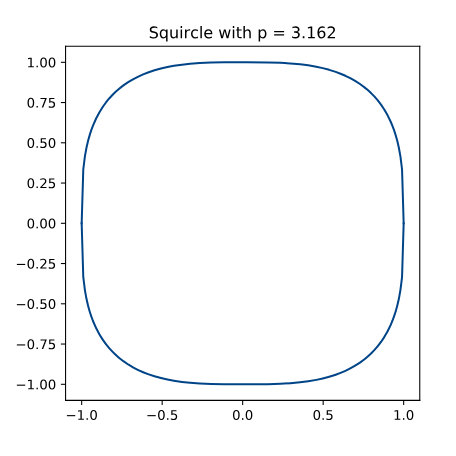
The circle is defined by the formula x2 + y2 =1, a
special case of the more general formula |x|n + |y|n =
1, where n may rise from 2 to any higher number. |
|
·
Already in the
summer of 1966, Peter named any resulting Supercircle a “Squircle”
(a
portmanteau of circle and square). http://www.geocities.ws/dougtclark/index-2.html#five |
|
As n converges to infinity
∞,
the circle converges to a square. In order to find the aesthetic middle
between a circle and a square, Peter posed the question: at which
ideal n in the formula |x|n + |y|n =1 does
the resulting Squircle reache a stage such that one cannot decide, if the resulting “ideal”
Squircle is visually closer to a circle or a square. |
|
Initially, Peter used a pragmatic
approach and traced 20 Squircles with n rising from 2.1
to 4.1 (whereas 2.1 is clearly closer to a circle
and 4.1 is clearly closer to a square). He then engaged a dozen friends to
proceed with inspecting and judging the 20 Squircles which were
laid out near the edge of a long table in the office. Their opinion as to the
undecidable shape averaged at 3.1, very close to the number Pi (a vain hope,
as it turned out later). |
|
Peter Panholzer’s
authorship of the word “Squircle” was not
referenced on the Internet until many years later: |
|
https://darmamade.wordpress.com/2006/07/06/research-on-squircle/ |
|
Peter’s authorship of the term “Squircle”
in the summer of 1966 has been confirmed in writing by his employer, architect
Gerald
Robinson, who lives and works in |
|
Peter Panholzer wrote: Gerald is a living witness of the events in the summer of 1966 and my
invention of the word “Squircle”. In attempting to find the “ideal” value of n in the formula
for the Squircle |x|n +
|y|n =1, such that one cannot decide,
if the resulting “ideal” Squircle
is visually closer to a circle or a
square, e.g. a
quest of the Super–Squircle, I
realised this was a challenging aesthetic problem and decided to look for a solution
with the help of computers. The first computer used for this purpose
was at the |
|
Current references
(only two among many others): https://en.wikipedia.org/wiki/Squircle |
|
The
most recent reference is here https://www.johndcook.com/blog/2019/04/02/history-of-the-term-squircle/ |
|
|